
【百度百科定义】凸优化,或叫做凸最优化,凸最小化,是数学最优化的一个子领域,研究定义于凸集中的凸函数最小化的问题。
凸优化这个概念实际在研究中经常会遇到。包括在机器学习、控制领域等等。最小二乘其实就是一种通过凸优化来实现的问题。

凸表明的是下凸,也就是上凹,直观地讲,函数形为
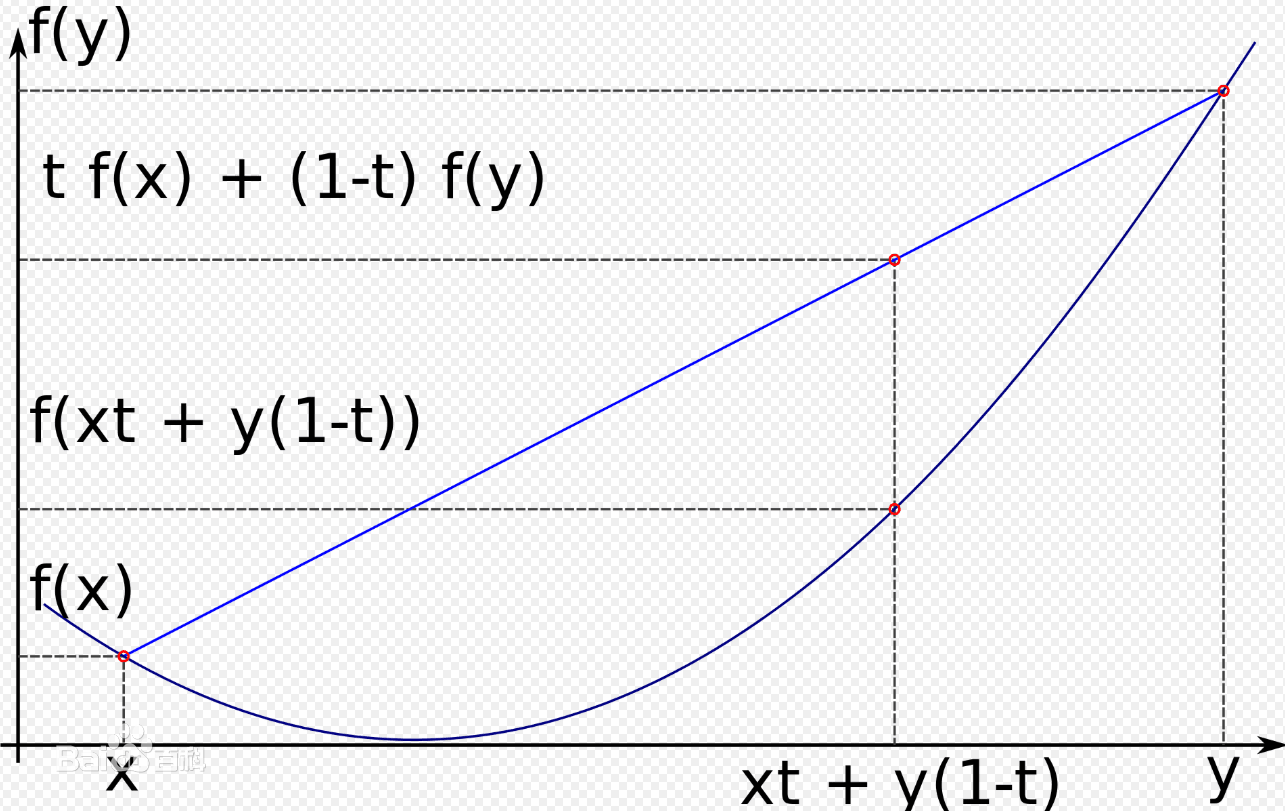
即为凸函数。
【百度百科】令S是实数上的线性空间,或者更一般地,是在某个有序域上,这包括欧几里德空间。如果对于C中的所有x和y,并且在区间(0,1)中的所有t,点 也属于C,则S中的集合C被称为凸。换句话说,连接x和y的线段上的每个点都在C中。这意味着实际或复杂拓扑线性空间中的凸集是道路连通的。
更易理解的说法:
设S为n维欧式空间
R
n
\mathbb{R} ^{n}
Rn中的一个集合,若对S中任意两点,联结它们的线段仍属于S,称这样的集合S是一个凸集。
用数学表达式来解释,即:
对S中任意两点
X
X
X,
Y
Y
Y, 及每个实数
λ
∈
[
0
,
1
]
\lambda \in [0,1]
λ∈[0,1],都有
λ
X
+
(
1
?
λ
)
Y
∈
S
\lambda X+(1-\lambda)Y \in S
λX+(1?λ)Y∈S,称为
X
,
Y
X, Y
X,Y的凸组合。
直白而不严谨的话说,对于任意两个点,连线上的任一点都在这个集合上,即为凸集。
举个例子:
1、直线,是凸集;
2、圆圈,不是凸集;
3、实心圆(饼),是凸集;
4、球体,是凸集。
机器学习简单来说,主要做的就是优化问题,先初始化一下权重参数,然后利用优化方法来优化这个权重,直到准确率不再是上升,迭代停止,那到底什么是最优化问题呢?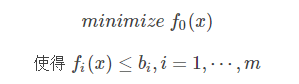
最小二乘问题是无约束的优化问题,通常可以理解为测量值与真实值之间的误差平方和:
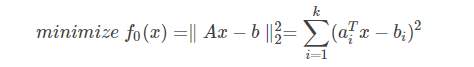
一张图就可以看得明白:

在线客服
客服咨询


官方微信
返回顶部