优化问题的目标函数中包含没有具体表达式的部分，该如何解这个优化问题？

形如

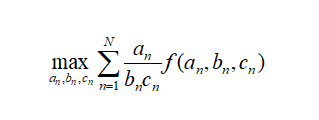
其中f(a,b,c)表示无法用显式表达式写出的部分，这样的优化问题怎么解？

补充：f(a,b,c)写不出具体表达式，但是f(a,b,c)的值与a,b,c映射关系已知，输入a,b,c可查表获得对应的f(a,b,c)值

data-driven optimization

问题的tag里把答案写得很清楚了。这是个黑盒优化，可以使用启发式方法

既然可以查表获取值，那么用doe算法多生成一些点，获取输出后，建立响应面函数，然后就可以基于响应面函数进行优化

首先图里的这个summation over n写的不清楚，需要题主修改函数f是如何与n相关的。

本质上可以归类为Black box optimization问题，解决办法之一，也是答主读博前两年一直在做的东西，是response surface method。即用一个response surface function（假设是函数g）去近似原函数f，通过迭代最小化g来优化给定的参数a，b和c去做sampling。也可以看作是一种data-driven optimization。

response surface由两部分组成，一部分是interpolation function，对原函数f做拟合，使得空间中已经sample过的a，b，c点处，f和g函数值相同。同时需要一个uncertainty function，对空间中未做过sampling的点做一个不确定度modeling，uncrtainty越大，越有可能给出极值。

这类问题本质NP hard，computational cost随decision variable的dimension的增加而exponentially增加。

属于典型的黑盒优化问题了。可以用启发式的算法，比如进化算法、遗传算法、粒子群算法等求解，这类算法可以容易地灵活处理离散变量和连续变量。

另一类就是用模式搜索、信赖域、坐标探测法、基于梯度的方法进行求解，需要注意对于离散变量梯度不可求去，或者存在偏差。

还有一类是基于模型的方法，采用插值函数、多项式等拟合模型去拟合目标函数或者局部拟合。另外也可以使用神经网络、随机森林、高斯过程等模型拟合目标函数，然后对模型求解最优值。如果模型能提供不确定性的量化输出，那还可以把预测方差添加到目标函数--也就是贝叶斯优化方法

需要指出，基于模型的方法本身存在一定的建模成本，预测精度也难以保证。所以要综合实际问题的维度、计算成本综合考虑使用哪种方法

• 上一篇: 抖音极速版是什么？
• 下一篇: 2017房地产十大新闻：史上最严厉调控政策密集出台