【DNN】模型的优化方法汇总--原理--优缺点--适用场景(Adagrad、ADAM、FTRL)

优化方法概述

1?SGD

2 Momentum

3.Adagrad

4.AdaDelta/RMSProp

5.ADAM(AdaptiVe Moment Estimation)

6.LazyAdam

7.Madam

到底是用Adam还是用SGD？

总结(究竟用什么优化方法)：

优化算法的常用tricks

3.FTRL（Follow the Regularized Leader）

---

深度学习优化算法有哪些？？面试中会问道优化问题，这里汇总一下：

m.set_linear_arg('FTRL', alpha=1e-4, lambda1=1e-6)
m.set_graph_arg('ADAM', alpha=1e-5, lambda2=1e-7)
m.set_embed_arg('SADAM', alpha=1e-5, lambda2=1e-7)

深度学习模型的发展进程：
SGD -> SGDM ->NAG -> AdaGrad -> AdaDelta -> Adam -> Nadam

模型优化方法的选择直接关系到最终模型的性能。有时候效果不好，未必是特征的问题或者模型设计的问题，很可能是优化算法的问题，而且好的优化算法还能够帮助加速训练模型。

在构建神经网络模型时，选择出最佳的优化器，以便快速收敛并正确学习，同时调整内部参数，最大程度地最小化损失函数。

Adam在实际应用中效果良好，超过了其他的自适应技术。

如果输入数据集比较稀疏，SGD、NAG和动量项等方法可能效果不好。因此对于稀疏数据集，应该使用某种自适应学习率的方法，且另一好处为不需要人为调整学习率，使用默认参数就可能获得最优值。

如果想使训练深层网络模型快速收敛或所构建的神经网络较为复杂，则应该使用Adam或其他自适应学习速率的方法，因为这些方法的实际效果更优。

理解指数加权平均

使得β=0.9

这是一个指数衰减的过程，这些系数的和为1或者逼近于1。到底平均了多少天的数据？也就是说，多久之内的数据是有效的，对m100的贡献更大呢？0.9 ^10大约为0.35，约等于1/e,也就是10天之后曲线的高度下降到1/3,相当于只关注了过去10天的数据,因为10天后，权重下降到不到当日权重的三分之一。如果β=0.98,那么0.98^50大约等于1/e,相当于关注了过去50天的数据。

总结：β越大，过去时段β对参数贡献的时长更久，更加依赖于过去时段的梯度。

偏差修正

现象：在初期更新梯度时，因为(1-β)较小，导致一阶动量更新缓慢；这也导致参数更新的比较缓慢。

计算移动平均数时，显然第一天的值会小很多，估计不准确；

偏差修正能够改正这个问题，特别是在初期。而当t足够大时，mt?=mt；

在计算指数加权平均数的大部分时候，都不在乎执行偏差修正，因为大部分人宁愿熬过初始时期，拿到具有偏差的估测，然后继续计算下去。如果关心初始时期的偏差，在刚开始计算指数加权移动平均数的时候，偏差修正能帮助在早期获取更好的估测。

优点：

快；容易实现；

缺点：

• 有可能会陷入局部最小值；
• 不会收敛，最终会一直在最小值附近波动，并不会达到最小值并停留在此；
• 下降速度慢；
• 选择合适的learning rate比较困难；
• 在所有方向上统一的缩放梯度，不适用于稀疏数据

SGD下降方法的缺点是参数更新方向只依赖于当前batch计算出的梯度，因此十分的不稳定。为了抑制SGD的震荡，动量认为梯度下降的过程中可以加入惯性。动量梯度下降法运行速度总是快于标准的梯度下降法，其基本思想是在SGD的基础上引入了一阶动量：

t时刻的下降方向，不仅由当前点的梯度方向决定，还由此前的累积的梯度来决定，β的经验值一般为0.9，也就是意味着下降方向主要是此前累积的下降方向，并略微偏向当前时刻的下降方向。并利用当前batch微调最终的更新方向。如果当前梯度方向与历史梯度一致，会增强该方向的梯度。如果不一致，能够减少更新。

优点：

• 增加了稳定性；
• 收敛速度更快；
• 还有一定摆脱局部最优的能力。

缺点：

SGD以及动量以同样的学习率更新每个参数。

之前的方法都没有用到二阶动量，二阶动量的出现，才意味着“自适应率”优化算法的到来。

适用场景--

Adagrad是一种基于梯度的优化算法：它将学习速率与参数相适应，对频繁参数的罕见更新和较小更新执行更大的更新。因此，它非常适合处理稀疏数据。AdaGrad是一种优化方法，它可以为不同的变量提供不同的学习率。它增加了罕见但信息丰富的特征的影响。

原理--

AdaGrad的基本思想是对每个变量用不同的学习率，这个学习率在一开始比较大，用于快速梯度下降。随着优化过程的进行，对于已经下降很多的变量，则减缓学习率，对于还没怎么下降的变量，则保持一个较大的学习率。怎么去度量历史更新频率呢？就是二阶动量：至今为止所有梯度值的平方和：

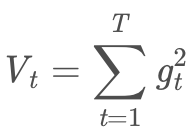
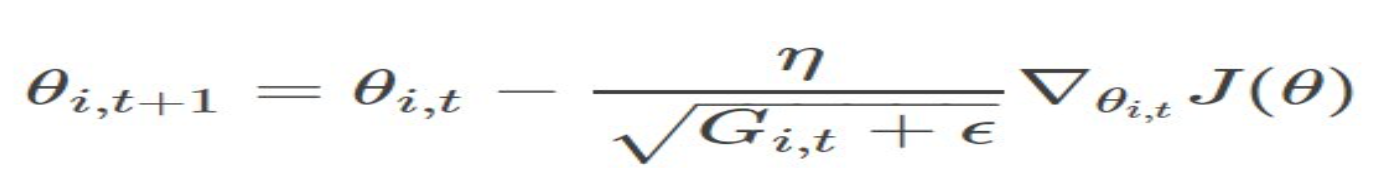
t代表每一次迭代。?一般是一个极小值，作用是防止分母为0 。G_i,t表示了前t 步参数θi梯度的平方累加.把沿路的Gradient的平方根，作为Regularizer。分母作为Regularizer项的工作机制如下：

★训练前期，梯度较小，使得Regularizer项很大，放大梯度。[激励阶段]

★训练后期，梯度较大，使得Regularizer项很小，缩小梯度。[惩罚阶段]

优点--

不同的变量提供不同的学习率。减少摆动，在稀疏数据场景下表现会非常好；

允许使用一个更大的学习率α，从而加快算法的学习速度；这个在后期，会通过分母来整体减小学习率。

缺点--

因为是不断累积单调递增的，会使得学习率单调递减至0，可能会使得训练过程提前结束，即使后续还有数据也无法学到需要的知识；

由于AdaGrad单调递减的学习率变化过于激进，我们考虑一个改变二阶动量计算方法的策略：不累加全部历史梯度，而只关注过去一段时间窗口的下降梯度，很自然的想到之前动量使用的指数加权平均，它所计算的就是过去一段时间的平均值，所以使用这一方法来计算二阶累积动量：

这就避免了二阶动量持续累积，导致训练过程提前结束的问题了。

Adam 最开始是由 OpenAI 的 Diederik Kingma 和多伦多大学的 Jimmy Ba 在提交到 2015 年 ICLR 论文（Adam: A Method for Stochastic Optimization）中提出的。

适用场景--

在使用大型模型和数据集的情况下，我们证明了?Adam?优化算法在解决局部深度学习问题上的高效性。

原理--

Adam?算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率（即?alpha）更新所有的权重，学习率在训练过程中并不会改变。而?Adam?通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。

Adam?算法的提出者描述其为两种随机梯度下降扩展式的优点集合，即：

• 适应性梯度算法（AdaGrad）为每一个参数保留一个学习率以提升在稀疏梯度（即自然语言和计算机视觉问题）上的性能。
• 均方根传播（RMSProp）基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。

本算法中有很多超参数，超参数学习率α很重要，也经常需要调试。β1和β2常用的缺省值为0.9和0.999。关于?的选择其实没那么重要，Adam论文的作者建议?=10^?8.

优点--

?Adam?优化算法在深度学习中的基本特性和原理：

• Adam?是一种在深度学习模型中用来替代随机梯度下降的优化算法。
• Adam?结合了?AdaGrad?和?RMSProp?算法最优的性能，它还是能提供解决稀疏梯度和噪声问题的优化方法。
• Adam?的调参相对简单，默认参数就可以处理绝大部分的问题。

缺点--

Adam有很多的优点，但是在很多数据集上的最好效果还是用SGD with Momentum细调出来的。可见Adam的泛化性并不如SGD with Momentum。https://arxiV.org/pdf/1711.05101.pdf 中提出其中一个重要原因就是Adam中L2正则化项并不像在SGD中那么有效。

1. L2正则和Weight Decay在Adam这种自适应学习率算法中并不等价，只有在标准SGD的情况下，可以将L2正则和Weight Decay看做一样。特别是，当与自适应梯度相结合时，L2正则化导致具有较大历史参数和/或者梯度幅度的权重比使用权重衰减时更小。这里作用于学习率，意思是加入L2正则后学习率变小了。
2. 使用Adam优化带L2正则的损失时，不work。如果引入L2正则化项，在计算梯度的时候会加上正则项求梯度的结果。正常的权重衰减是对所有的权重都采用相同的系数进行更新，本身比较大的一些权重对应的梯度也会比较大，惩罚也越大。但由于Adam计算步骤中减去项会有除以梯度平方的累积，使得梯度大的减去项偏小，从而具有大梯度的权重不会像解耦权重衰减那样得到正则化。 这导致自适应梯度算法的L2和解耦权重衰减正则化的不等价。

而在常见的深度学习库中只提供了L2正则，并没有提供权重衰减的实现。这可能就是导致Adam跑出来的很多效果相对SGD with Momentum有偏差的一个原因。

权重衰减（L2正则化项）为什么能够避免模型过拟合的问题？

奥卡姆剃刀法则；
过拟合模型的系数往往非常大，因为过拟合就是需要顾忌每一个点，最终形成的拟合函数波动很大，这就意味在某些小区间里的导数值非常大，也就是系数很大，而通过正则化约束参数的范数使其不要太大，可以在一定程度上减少过拟合情况。
?

LazyAdam是Adam的变体，可以更有效地处理稀疏更新。原始的Adam算法为每个可训练变量维护两个移动平均累加器，累加器在每一步都会更新。 而此类为稀疏变量提供了更加懒惰的梯度更新处理，它仅更新当前batch中出现的稀疏变量索引的移动平均累加器，而不是更新所有索引的累加器。 与原始的Adam优化器相比，它可以为某些应用提供模型训练吞吐量的大幅改进。 但是它的语义与原始的Adam算法略有不同，可能会导致不同的实验结果。

公式与Adam都相同，不同的是每次迭代根据当前batch的indices来对一阶动量和二阶动量进行更新。

Madam其实是介于Lazy Adam和 Adam之间的一种方法，其与Lazy Adam唯一的不同在于对一阶动量m和二阶动量 V 进行 decay 的操作，Madam是全部都要 decay，即当前batch没有采样到的变量所对应的之前动量的累积值也要考虑。 而LazyAdam 是只 decay 采样到的embedding。（在计算指数加权平均时，LazyAdam只对当前采样到的变量之前的平均值进行累加，没有采样到的样本不累加，而Madam要全部累加）。

LazyAdam存在的一个问题是当梯度为0时不更新对应的m和v。实际上当其他权重改变时m和v应该更新。Madam应该是解决了这个问题所以性能变得更好。
?

SGD虽然训练时间更长，容易陷入鞍点，但是在好的初始化和学习率调度方案的情况下，结果更可靠。SGD现在后期调优时还是经常使用到，但SGD的问题是前期收敛速度慢。SGD前期收敛慢的原因： SGD在更新参数时对各个维度上梯度的放缩是一致的，并且在训练数据分布极不均衡时训练效果很差。而因为收敛慢的问题应运而生的自适应优化算法Adam、AdaGrad、RMSprop 等，但这些自适应的优化算法泛化能力可能比非自适应方法更差，虽然可以在训练初始阶段展现出快速的收敛速度，但其在测试集上的表现却会很快陷入停滞，并最终被 SGD 超过。 实际上，在自然语言处理和计算机视觉方面的一些最新的工作中SGD（或动量）被选为优化器，其中这些实例中SGD 确实比自适应方法表现更好。
Adam的罪状一
这篇是正在深度学习领域顶级会议之一 ICLR 2018 的?On the ConVergence of Adam and Beyond，探讨了Adam算法的收敛性，通过反例证明了Adam在某些情况下可能会不收敛。

其中，SGD没有用到二阶动量，因此学习率是恒定的（实际使用过程中会采用学习率衰减策略，因此学习率递减）。AdaGrad的二阶动量不断累积，单调递增，因此学习率是单调递减的。因此，这两类算法会使得学习率不断递减，最终收敛到0，模型也得以收敛。

但AdaDelta和Adam则不然。二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得 Vt可能会时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

这篇文章也给出了一个修正的方法。由于Adam中的学习率主要是由二阶动量控制的，为了保证算法的收敛，可以对二阶动量的变化进行控制，避免上下波动。

使得学习率单调递减。

Adam的罪状二

深度神经网络往往包含大量的参数，在这样一个维度极高的空间内，非凸的目标函数往往起起伏伏，拥有无数个高地和洼地。有的是高峰，通过引入动量可能很容易越过；但有些是高原，可能探索很多次都出不来，于是停止了训练。

吐槽Adam最狠的?The Marginal Value of AdaptiVe Gradient Methods in Machine Learning?：同样的一个优化问题，不同的优化算法可能会找到不同的答案，但自适应学习率的算法往往找到非常差的答案。他们通过一个特定的数据例子说明，自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。

?ImproVing Generalization Performance by Switching from Adam to SGD，进行了实验验证。他们CIFAR-10数据集上进行测试，Adam的收敛速度比SGD要快，但最终收敛的结果并没有SGD好。他们进一步实验发现，主要是后期Adam的学习率太低，影响了有效的收敛。他们试着对Adam的学习率的下界进行控制，发现效果好了很多。

于是他们提出了一个用来改进Adam的方法：前期用Adam，享受Adam快速收敛的优势；后期切换到SGD，慢慢寻找最优解。这一方法以前也被研究者们用到，不过主要是根据经验来选择切换的时机和切换后的学习率。这篇文章把这一切换过程傻瓜化，给出了切换SGD的时机选择方法，以及学习率的计算方法，效果看起来也不错。

总结(究竟用什么优化方法)：

在充分理解数据的基础上，依然需要根据数据特性、算法特性进行充分的调参实验，找到最优解。

1. 首先，各大算法孰优孰劣并无定论。如果是刚入门，优先考虑SGD+NesteroV Momentum或者Adam.（Standford 231n : The two recommended updates to use are either SGD+NesteroV Momentum or Adam）
2. 选择你熟悉的算法——这样你可以更加熟练地利用你的经验进行调参。
3. 充分了解你的数据——如果模型是非常稀疏的，那么优先考虑自适应学习率的算法。如果在意更快的收敛，并且需要训练较深较复杂的网络时，推荐使用自适应学习率的优化方法。
4. 根据你的需求来选择——在模型设计实验过程中，要快速验证新模型的效果，可以先用Adam进行快速实验优化；在模型上线或者结果发布前，可以用精调的SGD进行模型的极致优化。
5. 先用小数据集进行实验——有论文研究指出，随机梯度下降算法的收敛速度和数据集的大小的关系不大。因此可以先用一个具有代表性的小数据集进行实验，测试一下最好的优化算法，并通过参数搜索来寻找最优的训练参数。
6. 考虑不同算法的组合：先用Adam进行快速下降，而后再换到SGD进行充分的调优。切换策略可以参考本文介绍的方法。
7. 数据集一定要充分的打散（shuffle）：这样在使用自适应学习率算法的时候，可以避免某些特征集中出现，而导致的有时学习过度、有时学习不足，使得下降方向出现偏差的问题。
8. 训练过程中持续监控训练数据和验证数据上的目标函数值以及精度或者AUC等指标的变化情况。对训练数据的监控是要保证模型进行了充分的训练——下降方向正确，且学习率足够高；对验证数据的监控是为了避免出现过拟合。
9. 制定一个合适的学习率衰减策略。可以使用定期衰减策略，比如每过多少个epoch就衰减一次；或者利用精度或者AUC等性能指标来监控，当测试集上的指标不变或者下跌时，就降低学习率。
10. ?

拓展：

2016年，Dozat, T.将 Nesterov Momentum算法的理念应用于Adam算法中，提出Nadam算法。Nadam对学习率有了更强的约束，同时对梯度的更新也有更直接的影响。

2018年，在Adam方法收敛到一个次优解时，观察到一些小批次样本贡献了大幅且有效的信息梯度，但是这种情况很少发生，指数平均后减小了它们的影响，导致模型收敛性差。Reddi等人提出AMSGrad算法对SGD算法进行改进.

参数更新方法记事，摘自机器之心：

能学习出有效的且稀疏的模型。对LR、FM这类模型的参数学习，传统的学习算法是batch learning算法，它无法有效地处理大规模的数据集，也无法有效地处理大规模的在线数据流。是一种有效且高效的online learning算法。

适用场景--

大规模机器学习，训练的数据量大，模型特征量的规模大。

优点--

SGD算法能学习出不错的模型，但学出的模型不是稀疏的。

FTRL能学习出有效的且稀疏的模型。FTRL算法融合了RDA算法能产生稀疏模型的特性和SGD算法能产生更有效模型的特性。它在处理诸如LR之类的带非光滑正则化项（例如1范数，做模型复杂度控制和稀疏化）的凸优化问题上性能非常出色，国内各大互联网公司都已将该算法应用到实际产品中。

原理--

核心内容：Wt+1 = Wt乘以历史梯度gs的和 + sigma*Wt与历史参数W差的二范数 + Wt的L1范数。

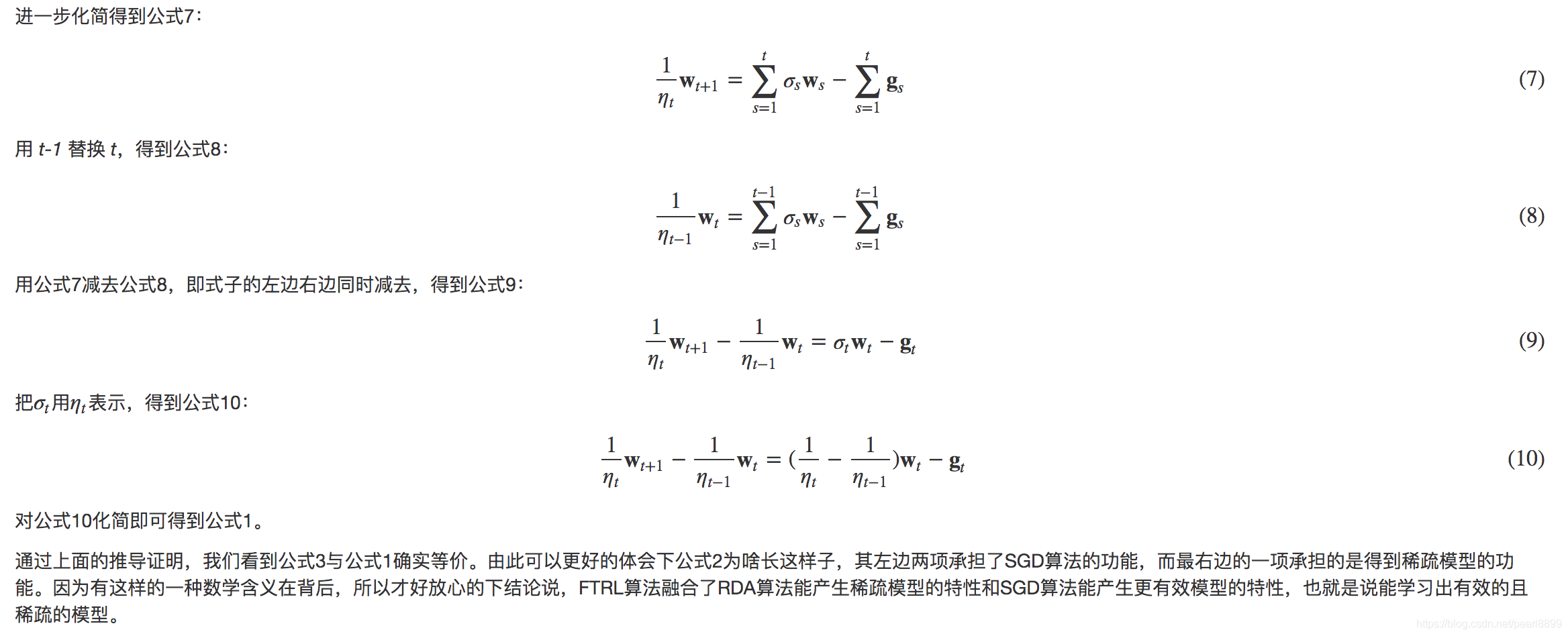
总结参数优化算法：

?

?

参考链接：

1.adagradhttps://www.jiqizhixin.com/graph/technologies/7eab38a3-23ec-494c-a677-415b6f85e6c5

2.https://www.jiqizhixin.com/articles/2017-07-12

3.FTRL讲的非常详细：http://vividfree.github.io/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/2015/12/05/understanding-FTRL-algorithm

4.手动深度学习，强烈推荐：https://zh.d2l.ai/chapter_optimization/momentum.html

5.常用优化器介绍的很全面：https://blog.csdn.net/yinyu19950811/article/details/90476956

• 上一篇: 悟饭游戏厅_1
• 下一篇: 抖音极速版19.2下载