
大家好,我是Luxury。公众号的一系列文章激发起了朋友们对数据运营的兴趣,甚至有朋友咨询如何才能实现高阶的数据运营。其实我认为之前的一系列文章都比较基础,只是协助大家梳理一些分析逻辑并建立一些模型评估而已,我认为高阶的数据运营应该是要将数学知识与工作、生活相互结合而应用,并不是追求数据工具的使用,也不是仅仅做一些逻辑分析的梳理,毕竟我也说过,任何的数据分析都是要建立在数理知识之上,否则那仅仅只是称之为数据的收集及整理罢了,要想成为一名合格的数据分析师,基本的数理知识是必不可少的。所以从今天开始,我会持续的分享一些数学知识(可能会涉及高等数学、线性代数、统计学、运筹学等等),同时结合国际站实际的运营场景,实操展示如何利用数学解决工作问题并进行延伸,今天首要分享的便是线性规划的理论知识及在国际站的实际应用。
一、业务场景提出
本篇的实操思路主要围绕该业务场景展开:如何摆脱“凭感觉”,科学的分配每个产品的P4P预算。在此先提出1个粉丝圈群友的典型问题:“每天预算300,P4P的平均单次点击花费为4块,原来在推的老品A反馈率为6%,现在经过产品累计分析模型挖掘了2个潜在产品B(反馈率18%)、C(反馈率15%),并打算将这两个产品加入推广,现在该如何分配这3个产品的预算才能使得询盘最大化?”
二、实操及分析流程理论解析
首先要给大家普及一下线性规划的基本概念,线性规划是运筹学的一个最重要的分支,主要用于研究有限资源的最佳分配问题,即如何对有限的资源作出最佳方式地调配和最有利地使用,以便最充分地发挥资源的效能去获取最佳的经济效益。
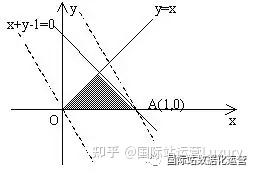
以上图为例,便是一个最基础的线性规划模型,由多个限制条件围成“可行域”(阴影部分),通过目标函数在可行域内找到最优解。线性规划的建模过程为:
①找到决策变量:根据影响所要达到目的的因素找到决策变量(即每个产品的预算);
②确定目标函数:由决策变量和所在达到目的之间的函数关系确定目标函数(即总体询盘的最大化);
③挖掘约束条件:由决策变量所受的限制条件确定所要满足的约束条件(即设定预算的前提条件)。
实操过程
第1步:建立线性规划模型
决策变量:设产品A、B、C的P4P预算分别为X1、X2、X3;
目标函数:设这3个产品的P4P总反馈为F,F=(X1/4)*6%+(X2/4)*18%+(X3/4)*15%,求F的最大值即F(Max);
约束条件:①预算约束:每天的预算须小于日限额,X1+X2+X3<=300
②老品A约束:由于老品A的流量构成稳定,因此不能使得A的付费流量波动过大,须保持原有付费点击的至少60%以上(原来的点击是300/4=75),即X1/4>=45③新品B、C约束:新品B、C属于测试性产品,需要保证每天不少于10个的点击从而达到积累数据的目的,即X2/4>=10、X3/4>=10
第2步:调用Excel的“规划求解”,得出最优分配结果
在Excel中将决策变量、约束条件、目标函数等设置好,各单元格的函数为:
A2、B2、C2:留空
D2:=A2+B2+C2

E2:=A2/4

F2:=B2/4G2:=C2/4H2:==(A2/4)*6%+(B2/4)*18%+(C2/4)*15%

设置完成后,选中单元格H2,点击“数据--规划求解”,如下图所示:
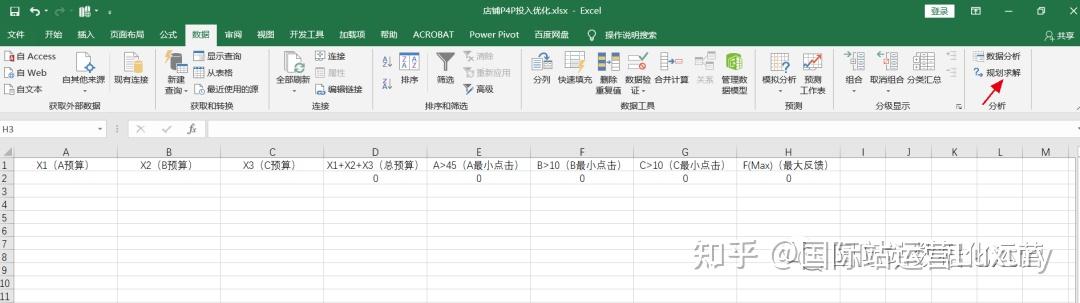
然后选中决策变量以及约束函数,如下图所示:
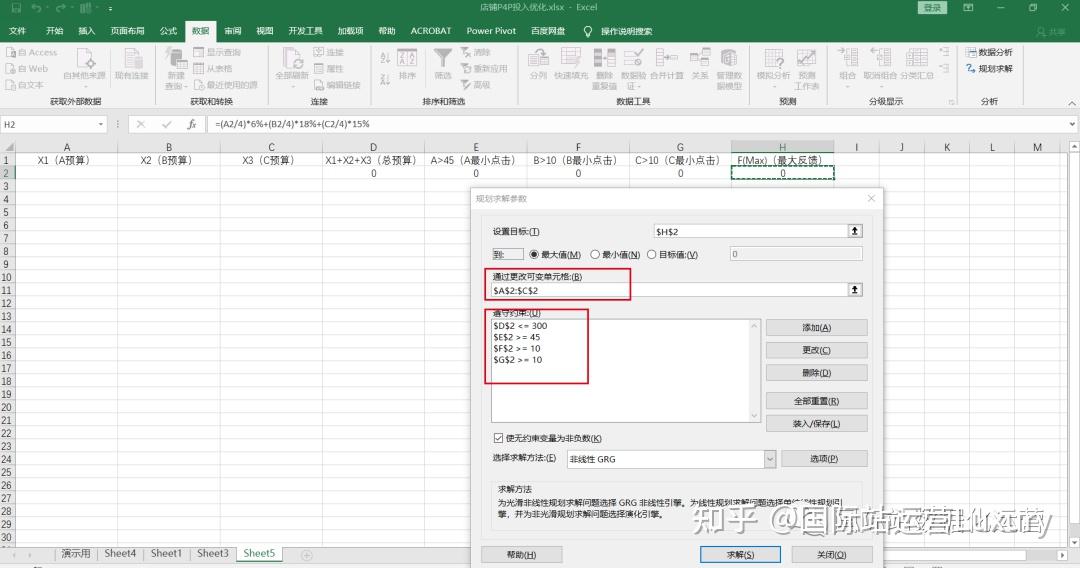
随后点击求解,即可得出每个产品的最优预算分配方案以及反馈最大值,如下图所示:

A品:180元、B品:80元、C品:40元,预计最大反馈量为10。
至此,我们利用数学原理,通过科学的方法完成了P4P预算的分配方案的制定,其实这虽然仅仅只是一个比较简单的案例,但又是我们每个人在实际运营当中会用遇到的决策问题,线性规划可以很好地协助我们在面临各种决策场景时,梳理出一套利益最大化的方案,而不是仅仅局限于这么一个小小的简单案例,更多的实际运营场景比如:
①整套国际站方案投入分配问题:P4P多少、顶展多少、问鼎多少等等
②信保的资源分配问题:各产品信保订单的绑定资源分配
③橱窗资源分配问题:应该将橱窗分配给哪些产品
④顶展资源分配问题:应该将顶展分配到哪些产品
⑤P4P资源分配问题:不同的推广类型如何分配预算、不同的关键词如何分配预算、不同的地域人群如何分配预算等等
⑥更多...
以上的场景都是我们在实际运营过程当中会面临的决策问题,如果能借助线性规划建立模型合理结合运用,可以有效地协助我们输出经济效益最大化的分配方案。与此同时,”找到决策变量-确定目标函数-挖掘约束条件“这一套规划建模思维价值很大,建议大家都去掌握,可以更科学地解决我们的决策难题,摆脱”凭感觉“。
推荐阅读:
优秀案例:数据化爆品打造及数据参谋拓品在线客服
客服咨询


官方微信
返回顶部